Modeling RL Problems

Disclaimer: The content for this article does not come from any textbook or other reliable sources. They are observations made purely from my very limited experience with RL.

I recommend that you gather some RL basics before you proceed to read this article. The first couple of posts from the course on my page could be a good start.

In this article, I’m going to talk about something that I haven’t seen anywhere before and nobody really talks about it but I’m going to take a shot at it. I’ve learned RL on my own and hence I’ve read several articles on the internet about RL but most of them are about the different algorithms starting from the most basic dynamic programming and going on till the most complex Soft Actor Critic. But having spent some time conducting RL research, I find that nobody really talks about, according to me, the most challenging and interesting problem in RL – the actual modeling of the problem.

So what do we mean by “modeling the problem”? If someone told you to solve the problem of self-driving cars using RL, how would you start? Lets say you decide to go ahead with some MDP framework, what would your states be? What would your actions be? What reward signal would you use? Would you solve the entire “self-driving” problem at once or would you want to break it down into smaller components? This is what I mean by “modeling a problem” and in my experience, has turned out to be the most important and challenging part of the bigger problem. Its something that sounds so simple but these early decisions are so important and I strongly believe that solid modeling could lead to better performance than using complex algorithms on weakly structured problems.

This is in fact one of the things that drew me to RL because I thought modeling problems was extremely interesting and challenging as well. I also couldn’t find anything quite similar to this in other domains. Feature selection in supervised learning comes close but there are specific techniques and tests you can conduct to come up with the best set of features given a large feature set. So this seemed like a unique problem specific to the RL world. But if it is such an exciting problem why hasn’t anyone written about it? My guess is that there is no simple answer to the question of “How to model an RL problem?”. The answer is that “It depends on the problem”. But I do believe there are some very simple guidelines you can follow or rather questions you can ask yourself when you’re modeling your problem. So here we go! Five questions that will help you model RL problems. There’s one additional question I guess that I’m implicitly answering; we will stick to the MDP framework and not talk about SMDPs or POMDPs for now (if you’ve never heard of these, good).

1. What are the actions I need?
2. Are my actions instantaneous?
3. What is my state space and can I make it smaller?
4. How complex is my problem and can I split it into smaller and easier problems?
5. What is the simplest reward function I can use?

So let’s go through them one by one.

What are the actions I need?

This is the first question you need to ask yourself when you’re handed a problem. What is the agent going to achieve and what actions will it need to achieve that task? This decision is often the easiest to make because this comes along with the problem description. So if the task is to navigate a car from one position of a square grid to another, the directions of movement would probably be the most natural choice for actions. Although this is much harder to see in a problem like Chess or self-driving cars, with a little bit of effort, we can think about all the different actions we have at our disposal. The important thing to keep track of however, is whether the action space is continuous or discrete and if discrete, how many actions you have. This information could be useful to decide if you maybe want to split the problem up into smaller easier problems. Remember, the more actions you have, the harder the task is.

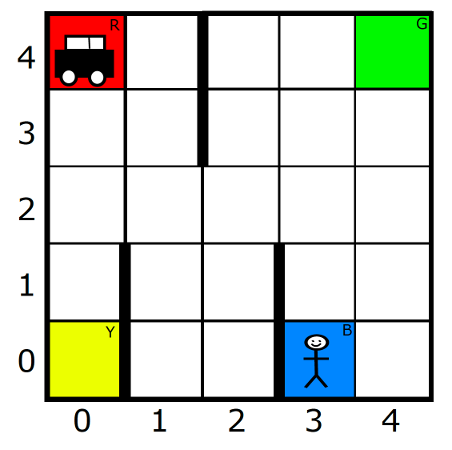
Are my actions instantaneous?

Once you’ve figured out what your actions are, we can take a closer look at them now. One thing we want to look for is whether the actions are instantaneous or not. Sometimes there could be actions that realistically take time to execute. For example, in the above car-grid problem, if your actions were “move the car to the green square”, this action could take time to execute realistically. Modeling them as aneous actions wouldn’t be accurate. In the MDP framework, we need all actions to be instantaneous. So what do we do when we have actions that take time? First, try to get rid of them or replace them with simpler instantaneous actions. But this is a trade-off because this could increase the number of actions. Next, think about whether the “long” action could be a separate problem on its own and that could be modeled as a separate smaller RL problem. But this starts getting into hierarchical RL and I wouldn’t get into it unless you’re sure about what I’m doing. One thing that I’ve done in the past to model actions that take time (that could even vary, every time the action is played) is to model time using probabilities and put a variable in the state space (we’ll get to this) indicating that the current action is in progress. So where do the probabilities come into play? Lets say a “long” action is in progress. Now we keep playing an extra “WAIT” action or “NOP” action and flip a coin (not a fair one) and if its heads, the “long” action ends. This seems convoluted but I’ve found that sometimes it could make life a lot simpler by introducing not too much complexity into the state space or action space. Otherwise, simply foraying into SMDPs and hierarchical RL is fine as well if you’re confident.

What is my state space and can I make it smaller?

So what variables are important for my problem and what goes into my state space? The crucial step here is to think about your actions. What variables do you need to decide what action you want to play in each state? Even thinking about what information a human might need could be useful. The key is to be minimalistic. Use as few variables as possible and use variables that don’t take too many values. Try to maintain a small, discrete state space. This is almost always never possible but its definitely worth the shot. If you can model a problem that you can solve with one of the basic RL algorithms without getting into function approximation (for the uninitiated, think of it as using deep learning), there’s nothing like it. But this is difficult and one of the hardest parts of the modeling problem. It takes a long time at the start of your project and it could get frustrating because you’re working with a white board and a marker and not a keyboard and a monitor. But trust me, the effort will be worth it. If you can design a small, simple state space then half the battle is won. At USC, when I was modeling my problem, it took over two weeks but we reduced our state space from over 33 billion to just 1440!

How complex is my problem and can I split it into smaller and easier problems?

I’m afraid there is no easy way to answer this that applies to all RL problems. But let me give you an example that might help. If I’m trying to make a robot learn to play tennis, I might want to split the big problem into smaller problems of “learning how to serve” or “learning how to play a forehand”, etc. One way of figuring out whether your problem needs breaking down is to check if all the actions make sense with each other i.e. can you play all actions at almost all states? Do you need all the state variables to make a call on whether you want to play an action or can I judge some actions just based on a subset of state variables? These questions may help you partition your state space and action space into multiple simpler problems that will make it easy to learn. Its not always easy to find these patterns and partitions though. And you also need to make sure there is an easy way to put these sub-problems back together. Nevertheless, if your problem is too complex i.e. too many states and/or too many actions then maybe it is worth spending the time solving multiple problems.

What is the simplest reward function I can use?

And finally, my favourite question. Questions 3 and 5 are by far the hardest of the lot and this question is probably the hardest of the lot. Which makes writing the answer so much easier. Researchers have recognized the difficulty of crafting reward functions and created a new field called Inverse Reinforcement Learning just to address the issue. But once again, there are some guidelines you can follow. Usually, I try to stick to the simplest reward function possible. What do I mean by simplest? Small values and as sparse as possible. So if I’m designing a reward function for chess, my rewards would only be at the end of the game and would be a +1, 0, -1 for a win, draw and loss respectively. Another reward function could be for every move played but this would be harder to craft and there’s no reason for you to try this until you know the simple reward function doesn’t work. But in the problem of chess, it is qite straight-forward but there are other problems where finding an elegant reward function might not be as simple.

So there you have it. I hope that helped and hopefully when you model your next problem, these tips will help. But thinking about all of this modeling has made me think about inverse reinforcement learning and meta learning a lot more. Is it possible for RL models to learn the optimal design of a problem? Not just the reward function but also the state space and the action space? And if it can, can it learn some common properties that we can learn across all RL problems? These are tough questions that I hope to answer some day.